6. Récursivité [en option]¶
Ce chapitre est prévu en tant que chapitre optionnel. Il présente un autre algorithme de tri célèbre, le Tri par fusion. Cet algorithme utilise la récursivité, une stratégie qui consiste en ce qu’un algorithme s’invoque lui-même. La récursivité, c’est un peu comme si on essayait de définir le terme « définition » en disant c’est une phrase qui nous donne la définition de quelque chose. C’est certes circonvolu que de vouloir utiliser dans une définition la chose-même que l’on est en train de définir, mais si on respecte quelques conditions, « ça fonctionne » !
6.1. Tri par fusion¶
Un autre algorithme de tri célèbre, inventé par John von Neumann en 1945, est le Tri par fusion. L’algorithme se base sur l’idée qu’il est difficile de trier un tableau avec beaucoup d’éléments, mais qu’il est très facile de trier un tableau avec juste deux éléments. Il suffit ensuite de fusionner les plus petits tableaux déjà triés.
L’algorithme commence par une phase de division : on divise le tableau en deux, puis on divise à nouveau les tableaux ainsi obtenus en deux, et ceci jusqu’à arriver à des tableaux avec un seul élément (voir la Figure ci-dessous). Comme pour la recherche binaire, le nombre d’étapes nécessaires pour arriver à des tableaux de 1 élément, en divisant toujours par deux, est log(n).
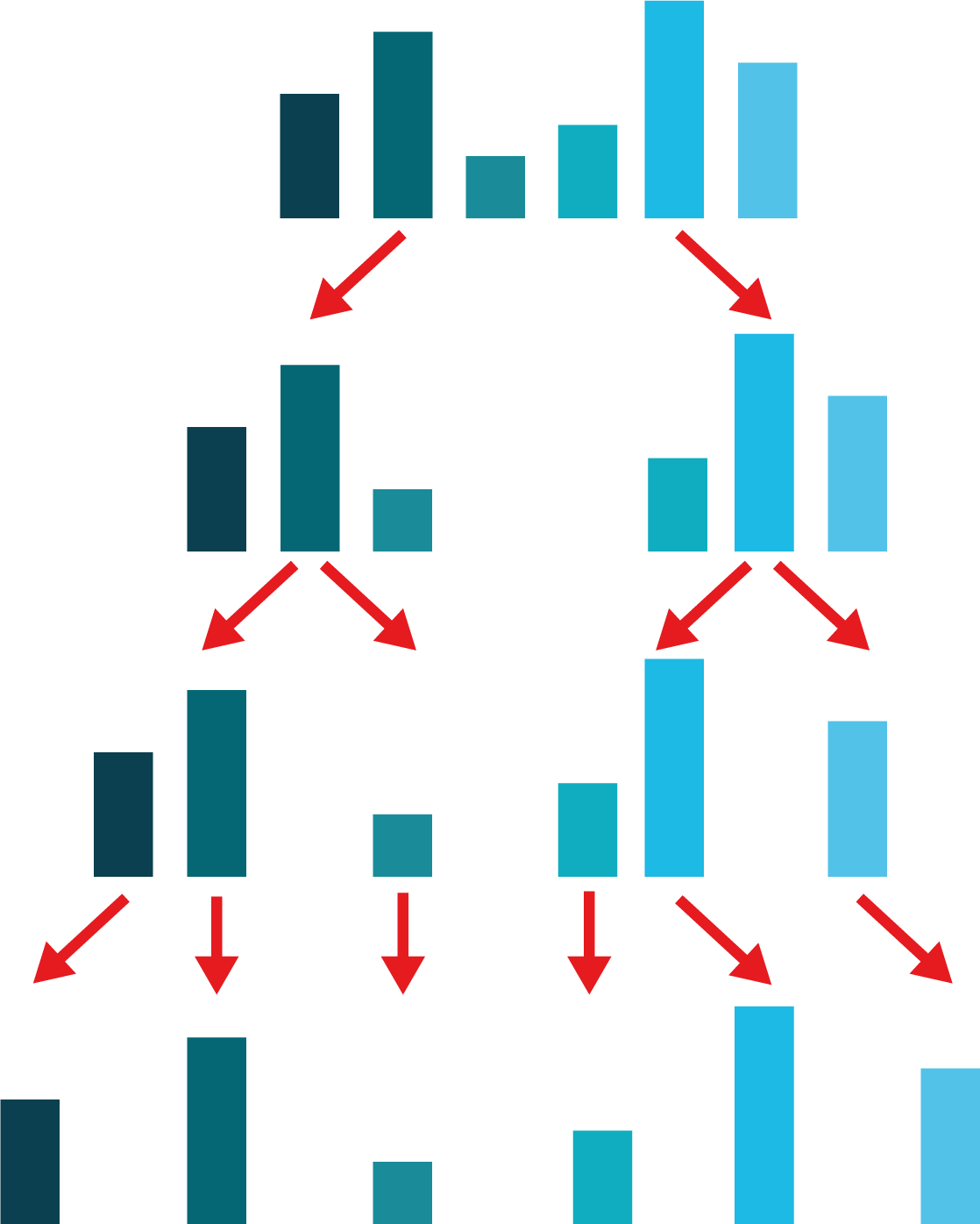
Phase de division. Illustration de la première phase du Tri par fusion : on commence par diviser le tableau en deux, puis à chaque étape on divise à nouveau les tableaux ainsi obtenus par deux, jusqu’à ce qu’il n’y ait plus que des tableaux à 1 élément.¶
La deuxième phase de fusion commence par fusionner des paires de tableaux à un élément, dans un ordre trié. Il suffit d’assembler les deux éléments du plus petit au plus grand, comme on peut le voir sur la 2e ligne de la figure ci-dessous. Dans les prochaines étapes, on continue à fusionner les tableaux par paires de deux, tout en respectant l’ordre de tri (lignes 3 et 4 de la figure). On continue de la sorte jusqu’à ce qu’il n’y ait plus de tableaux à fusionner.
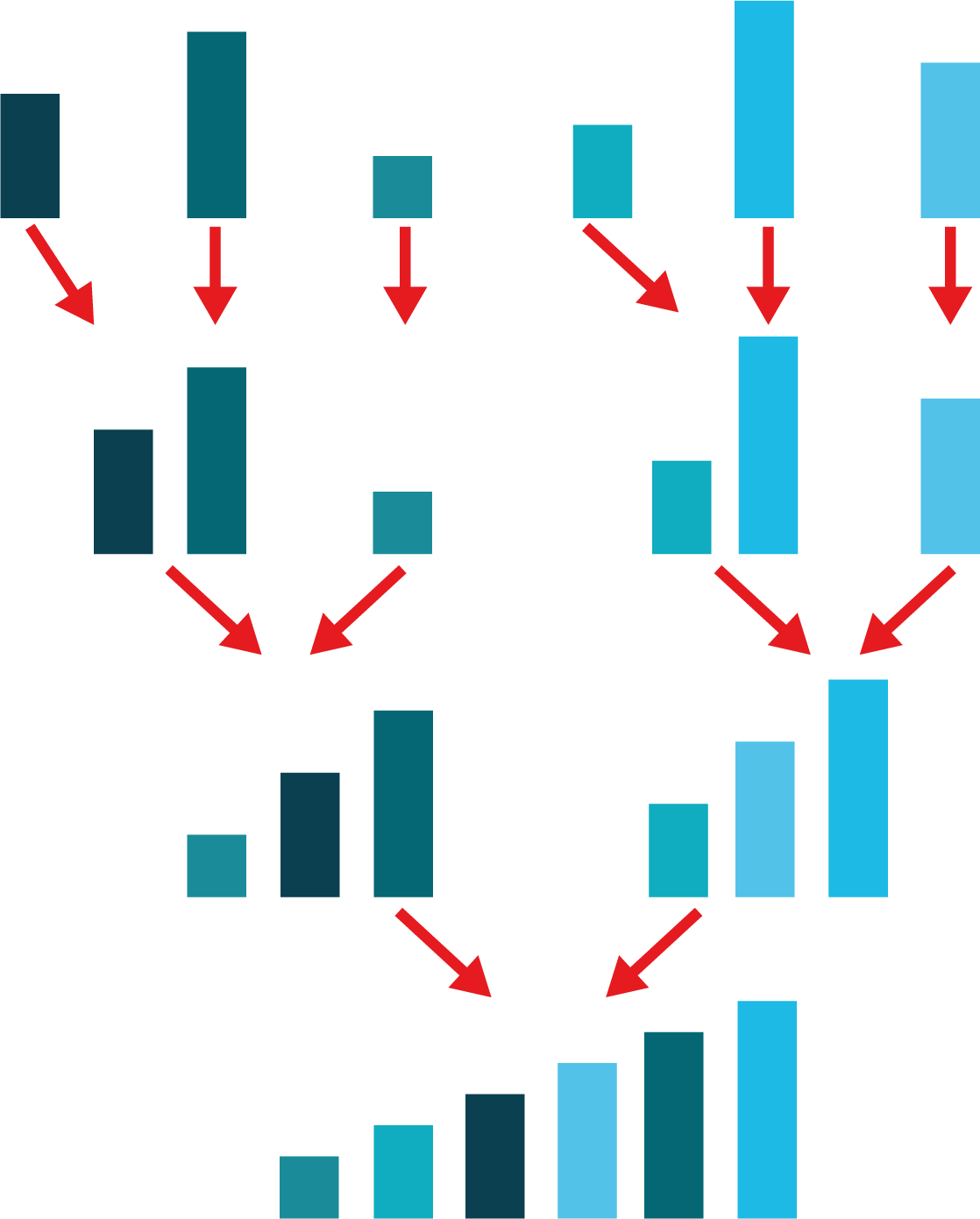
Phase de fusion. Illustration de la deuxième phase du Tri par fusion : on commence par fusionner les tableaux à un élément, en faisant attention à respecter l’ordre de tri (ligne 2) ; puis par fusionner à nouveau les tableaux obtenus à l’étape précédente, toujours en respectant l’ordre de tri (lignes 3 et 4). On continue de la sorte jusqu’à ce qu’il n’y ait plus qu’un tableau unique (ligne 4).¶
La fusion de tableaux déjà triés, par rapport à des tableaux non-triés, est très facile. Il suffit de comparer les premiers éléments des deux tableaux à fusionner et de prendre le plus petit des deux. Concrètement, on enlève le plus petit élément des deux tableaux pour le mettre dans le nouveau tableau fusionné. On compare ensuite les premiers éléments de ceux qui restent dans les tableaux à fusionner et on prend à nouveau le plus petit des deux pour le mettre à la suite dans le tableau fusionné.
Chaque étape de la phase de fusion consiste à comparer deux éléments n fois, autant de fois qu’il y a d’éléments à fusionner. Le temps de calcul grandit donc linéairement en fonction de la taille du tableau n (plus il y a d’éléments dans le tableau, plus la fusion prend du temps). En tout il y a besoin de log(n) étapes (fusion deux par deux), dont chacune prend un temps qui dépend de n, ce qui nous donne un ordre de complexité linéarithmique.
Pour aller plus loin
Même si le tri rapide et le tri fusion ont la même complexité temporelle, c’est-à-dire qu’ils prennent un temps comparable pour trier des données, le tri rapide prend beaucoup moins de place en mémoire. On dit qu’il a une plus petite « complexité spatiale ».
6.2. 4.1 Focus sur la récursivité¶
Nous allons maintenant programmer l’algorithme du Tri par fusion. Pour rappel, la première phase de l’algorithme divise continuellement le tableau par deux, comme illustré dans la première figure ci-dessus. Voici le code qui permet de diviser un tableau en deux une seule fois :
# Tri par fusion
def tri_par_fusion(elements):
### Phase DIVISION
# détermine l'indice au milieu du tableau (division entière)
milieu = len(elements)//2
# prend tous les éléments depuis le début, jusqu'à (et sans) milieu
elements_gauche = elements[:milieu]
# prend tous les éléments depuis le milieu (y compris), jusqu'à la fin
elements_droite = elements[milieu:]
La division utilisée pour déterminer le milieu du tableau est une division entière // au lieu de /. En effet, on souhaite obtenir un résultat entier et non un nombre à virgule, car les indices pour accéder aux éléments du tableau doivent être des entiers. Par exemple, si le tableau contient 5 éléments, cela n’aurait pas de sens de prendre les premiers 2.5 éléments, et 5//2 nous retournerait 2.
Ce qui suit est très intéressant. Dans l’étape d’après, on souhaite faire exactement la même chose pour les nouveaux tableaux elements_gauche (équivalent à elements[:milieu]) et elements_droite (équivalent à elements[milieu:]), c’est-à dire que l’on souhaite à nouveau les diviser en deux, comme sur la deuxième ligne dans la première figure ci-dessus. On va donc appeler la fonction tri_par_fusion sur les deux moitiés de tableaux :
# Tri par fusion
def tri_par_fusion(elements):
### Phase DIVISION
# détermine l'indice au milieu du tableau (division entière)
milieu = len(elements)//2
# prend tous les éléments depuis le début, jusqu'à (et sans) milieu
elements_gauche = tri_par_fusion(elements[:milieu])
# prend tous les éléments depuis le milieu (y compris), jusqu'à la fin
elements_droite = tri_par_fusion(elements[milieu:])
Regardez bien ce qui se passe. Nous avons fait appel à la même fonction tri_par_fusion que l’on est en train de définir ! Pour l’instant cette fonction ne fait que diviser le tableau elements en deux, elle va donc diviser le tableau reçu en entrée en deux. Au début le tableau en entrée sera le tableau entier, mais ensuite il s’agira des deux moitiés du tableau, puis des moitiés de la moitié et ainsi de suite. La fonction tri_par_fusion appelle la fonction tri_par_fusion (elle s’appelle donc elle-même), qui va à nouveau s’appeler et ainsi de suite…
Si on laisse le programme tel quel, on est face à un problème. La fonction tri_par_fusion continue de s’appeler elle-même et ce processus ne s’arrête jamais. En réalité, il faut arrêter de diviser lorsque les tableaux obtenus ont au moins un élément ou lorsqu’ils sont vides, car dans ces cas on ne peut plus les diviser en deux. On rajoute donc cette condition d’arrêt de la récursion :
# Tri par fusion
def tri_par_fusion(elements):
### Phase DIVISION
# condition d'arrêt la récursion
if len(elements) <= 1:
return(elements)
# détermine l'indice au milieu du tableau (division entière)
milieu = len(elements)//2
# prend tous les éléments depuis le début, jusqu'à (et sans) milieu
elements_gauche = tri_par_fusion(elements[:milieu])
# prend tous les éléments depuis le milieu (y compris), jusqu'à la fin
elements_droite = tri_par_fusion(elements[milieu:])
Voici le programme appliqué sur l’exemple de la figure. Essayez de comprendre dans quel ordre sont appelées les fonctions tri_par_fusion et avec quel paramètre en entrée. Pour une meilleure visibilité, nous affichons l’état des variables avec print.
Une fonction qui s’appelle elle-même est appelée fonction récursive. Il s’agit d’une mise en abime, d’une définition circulaire. Lorsqu’on entre dans la fonction, des opérations sont exécutées et on fait à nouveau appel à la même fonction, mais cette fois-ci avec d’autres éléments en entrée, afin de refaire les mêmes opérations, comme le montre cette figure :

Schéma d’une fonction récursive. La fonction s’appele elle-même. toujours avec un autre paramètre en entrée, jusqu’à ce que la condition d’arrêt soit remplie. A ce moment-là, un résultat est calculé et retourné à la fonction du dessus (celle qui à appelé la fonction). Ainsi tous les résultats sont retournés au fur et à mesure et permettent de calculer la fonction souhaitée.¶
Les deux ingrédients indispensables à toute fonction récursive sont donc :
un appel à la fonction elle-même à l’intérieur de la définition de la fonction.
une condition d’arrêt, qui permet de terminer les appels imbriqués.
Exercice 4.0. Position de la condition d’arrêt
Sans la condition d’arrêt, un programme récursif ne se termine pas, et s’appelle soi-même indéfiniment. Il est important que cette condition d’arrêt précède l’appel récursif à la fonction. Pourquoi est-ce le cas ?
Solution 4.0. Position de la condition d’arrêt
Maintenant que nous avons programmé la première phase de division du Tri par fusion il nous faut programmer la deuxième phase de fusion (voir la deuxième figure du Tri par fusion). Nous allons définir cette phase de fusion de manière récursive :
# Phase de fusion du Tri par fusion
def fusion(elements_gauche, elements_droite):
# trouve le plus petit premier élément des deux listes
if elements_gauche[0] < elements_droite[0]:
# appelle fusion récursivement avec le reste des listes
elements_reste = fusion(elements_gauche[1:], elements_droite)
# crée une liste fusionnée avec le résultat
elements_fusion = [elements_gauche[0]] + elements_reste
else:
# appelle fusion récursivement avec le reste des listes
elements_reste = fusion(elements_gauche, elements_droite[1:])
# crée une liste fusionnée avec le résultat
elements_fusion = [elements_droite[0]] + elements_reste
return(elements_fusion)
Quelle est la différence entre le code dans la partie if de la condition et dans la partie else de la condition ? Lorsqu’on fusionne deux tableaux qui sont déjà triés, le plus petit élément se trouve parmi les premiers éléments des deux tableaux à fusionner. On commence alors par prendre le plus petit des premiers éléments des deux tableaux à fusionner, que l’on met au début de notre tableau fusionné. On refait ensuite la même opération avec le reste des éléments : on sélectionne le plus petit élément des tableaux de départ et on le met à la suite de notre tableau fusionné. On recommence de la sorte tant qu’il n’y ait plus d’éléments dans les tableaux.
Dans la partie if de la fonction fusion, c’est le tableau de gauche qui contient le plus petit élément. On prend cet élément pour le mettre au début d’un nouveau tableau fusionné et on appelle la fonction fusion sur les éléments restants. Dans la partie else on fait la même chose, sauf que l’on commence notre tableau fusionné par le premier élément du tableau de droite.
Mais n’y a-t-il pas quelque chose qui manque à cette fonction ? En effet, il manque la condition d’arrêt. Il faut arrêter la fusion lorsqu’un des deux tableaux à fusionner est vide. Dans ce cas la solution de fusionner un tableau vide avec un autre tableau est triviale : c’est l’autre tableau non vide. Mettons ceci sous forme de code :
# Phase de fusion du Tri par fusion
def fusion(elements_gauche, elements_droite):
# conditions d’arrêt de la récursivité
if elements_gauche == []:
return(elements_droite)
if elements_droite == []:
return(elements_gauche)
# trouve le plus petit premier élément des deux listes
if elements_gauche[0] < elements_droite[0]:
# appelle fusion récursivement avec le reste des listes
elements_reste = fusion(elements_gauche[1:], elements_droite)
# crée une liste fusionnée avec le résultat
elements_fusion = [elements_gauche[0]] + elements_reste
else:
# appelle fusion récursivement avec le reste des listes
elements_reste = fusion(elements_gauche, elements_droite[1:])
# crée une liste fusionnée avec le résultat
elements_fusion = [elements_droite[0]] + elements_reste
return(elements_fusion)
Pour que le programme soit complet, il faut faire appel cette fonction fusion dans la fonction tri_fusion ci-dessus :
# Tri par fusion
def tri_par_fusion(elements):
### Phase DIVISION
# condition d'arrêt la récursion
if len(elements) <= 1:
return(elements)
# détermine l'indice au milieu du tableau (division entière)
milieu = len(elements)//2
# prend tous les éléments depuis le début, jusqu'à (et sans) milieu
elements_gauche = tri_par_fusion(elements[:milieu])
# prend tous les éléments depuis le milieu (y compris), jusqu'à la fin
elements_droite = tri_par_fusion(elements[milieu:])
# fusionne les éléments un par un, puis deux par deux, etc..
resultat = fusion(elements_gauche, elements_droite)
# retourner le résultat
return(resultat)
Ces deux fonctions ensemble implémentent l’algorithme du Tri par fusion de manière récursive. La récursivité est un concept difficile à appréhender. Le mieux est d’essayer de coder différents algorithmes récursifs et d’afficher ce qui se passe au fur et à mesure. Voici le programme appliqué sur l’exemple de la figure :
6.3. Exercices supplémentaires¶
Exercice 4.1 Fractale 🔌
Une fractale est un objet géométrique, dont la définition récursive est naturelle. Essayez le code suivant pour différentes valeurs de n (augmenter à chaque fois de 1).
Essayez de comprendre comment le flocon se construit de manière récursive. Vous pouvez aussi varier la longueur du segment dessiné et la vitesse d’affichage en décommentant la ligne correspondante.
Exercice 4.2. Une question de fusion
Trier le tableau suivant avec l’algorithme de tri par fusion : [3, 6, 8, 7, 1, 9, 4, 2, 5] à la main. Représenter l’état du tableau lors de toutes les étapes intermédiaires.
Exercice 4.3. Dans l’autre sens 🔌
En Python, proposer une fonction qui inverse l’ordre des lettres dans un mot. Vous pouvez parcourir les lettres du mot directement ou à travers un indice.
Proposer une autre fonction qui inverse l’ordre des lettres dans un mot de manière récursive.
Exercice 4.4. Factorielle 🔌
La fonction factorielle n! en mathématiques est le produit de tous les nombres entiers jusqu’à n. C’est une des fonctions les plus simples à calculer de manière récursive. Elle peut être définie comme ceci :
n! = (n-1)! * n
Programmer cette fonction de manière récursive en Python. Proposer également une implémentation itérative de la factorielle où les éléments de 1 à n sont traités l’un après l’autre.