18. Trier - sort()

Dans ce chapitre, nous allons découvrir quelques algorithmes de tri. Pouvoir trier les éléments d’une liste est une fonctionnalité fondamentale dans l’informatique. Le succès énorme de Google est basé sur un tri efficace de l’information, car dans une liste triée on peut trouver un élément beaucoup plus vite. Nous allons voir que :

• la fonction min(liste) retourne le minimum,

• la fonction max(liste) retourne le maximum,

• la méthode liste.sort() trie une liste.

Lorsque vous jouez aux cartes, vous triez vos cartes par valeur et dans ce cas, vous utilisez sans le savoir un algorithme de tri.

18.1. Fonction min et max

Les fonctions min() et max() retournent le minimum et le maximum d’une liste à l’aide d’un algorithme.
Mais comment fonctionne cet algorithme ?

Exercice : Modifiez la liste avec de nouvelles valeurs et essayez de nouveau.

18.2. Trouver le minimum

Pour trouver le minimum dans une liste il faut :

• prendre la première valeur comme minimum courant,

• parcourir le reste de la liste,

• garder la valeur comme nouveau minimum si elle est plus petite.

Exercice : Modifiez l’algorithme pour trouver le minimum ET le maximum.

18.3. Créer une liste

Pour visualiser les algorithmes que nous allons rencontrer dans ce chapitre, nous allons créer des listes avec des nombres aléatoires.

Avec une compréhension nous allons créer :

• une liste x avec des valeurs équidistantes dans l’intervalle [-300, 300]

• une liste y avec des valeurs aléatoires dans l’intervalle [-200, 200]

Exercice : Modifiez n à 14.

18.4. Visualiser une liste

Nous utilisons les listes x et y pour afficher des points et visualiser la liste y.

Exercice Modifiez le nombre d’éléments.

18.5. Visualiser un algorithme

Pour visualiser l’algorithme du minimum, nous dessinons en rouge les valeurs du minimum courant. Cet algorithme :

• prend la première valeur comme minimum courant,

• parcourt le reste de la liste,

• garde la valeur comme nouveau minimum si elle est plus petite.

Exercice : Modifiez l’algorithme pour visualiser le minimum ET le maximum.

18.6. L’indice du minimum

Souvent, on ne doit pas seulement trouver la valeur minimum, mais aussi son indice dans la liste. Contrairement au cas précédent, ici nous ne parcourons pas les valeurs, mais les indices.

Exercice : Modifiez l’algorithme pour trouver l’indice du minimum ET maximum.

18.7. Échanger deux éléments

Pour échanger deux éléments d’une liste, nous utilisons une affectation multiple. Ici nous échangeons les deux premiers éléments, donc les éléments avec les indices 0 et 1.

Le programme devient plus lisible si nous définissons une fonction echange().

18.8. Déplacer un point

Pour visualiser le déplacement d’un point de l’indice i vers l’indice j nous effaçons le premier point en le dessinant en blanc, et nous indiquons avec une ligne le déplacement vers la nouvelle position.

18.9. Échanger deux points

Pour échanger deux points, il faut :

• déplacer point i vers j

• déplacer point j vers i

• échanger les deux éléments dans la liste

18.10. Échanger tous les points

Dans l’exemple suivant, nous échangeons deux points successifs pour toute la liste. Nous observons que :

• le premier point avance complètement de gauche à droite

• tous les autres points reculent d’une position

18.11. Tri par sélection

L’algorithme du tri par sélection commence par rechercher le plus petit élément de la liste et l’échange avec le premier élément de la liste.

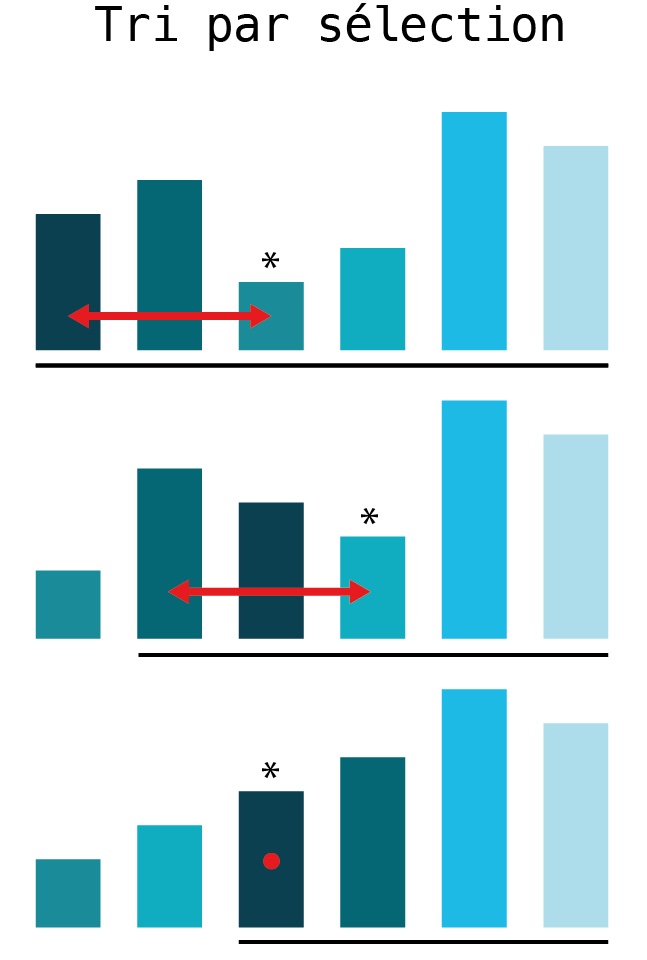
Il recherche ensuite le plus petit élément de la liste restante. Il sélectionne ainsi le deuxième plus petit élément de la liste et l’échange avec le deuxième élément de la liste. Et ainsi de suite.

Avec les fonctions min() et index() nous pouvons écrire cet algorithme de façon encore plus compacte.

Voici une visualisation du tri par sélection.

Exercice : Modifiez la taille de la liste.

18.12. Tri par insertion

L’algorithme du tri par insertion est utilisé par la plupart des personnes pour trier des cartes à jouer. On prend les cartes non triées depuis la table, et on les insère à l’endroit correct dans sa main.

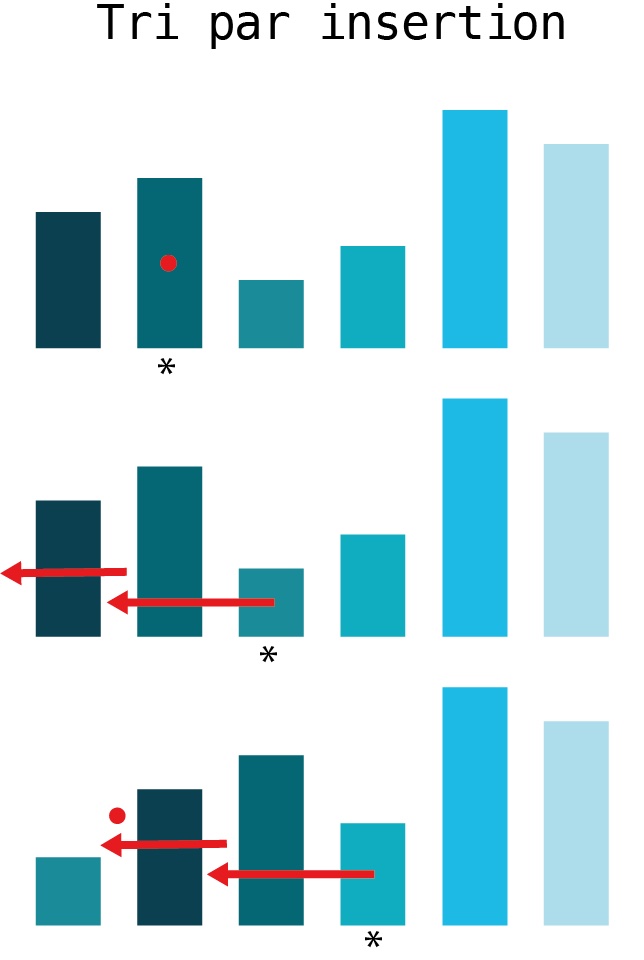
L’algorithme du tri par insertion parcourt la liste d’éléments à trier du deuxième au dernier élément. Pour chaque nouvel élément considéré, il l’insère à l’emplacement correct dans la liste déjà parcourue.

Voici une visualisation du tri par insertion.

Exercice : Modifiez la taille de la liste.

18.13. Tri à bulles

L’algorithme du tri à bulles compare les éléments voisins, deux par deux, et les met dans le bon ordre. Le mot ‘bulles’ fait référence aux bulles dans une boisson qui montent à la surface.

Dans l’exemple suivant, nous pouvons voir comment le 4 flotte vers le haut, jusqu’à ce qu’il rencontre le le 6 qui monte alors tout vers la surface, comme des bulles dans une boisson.

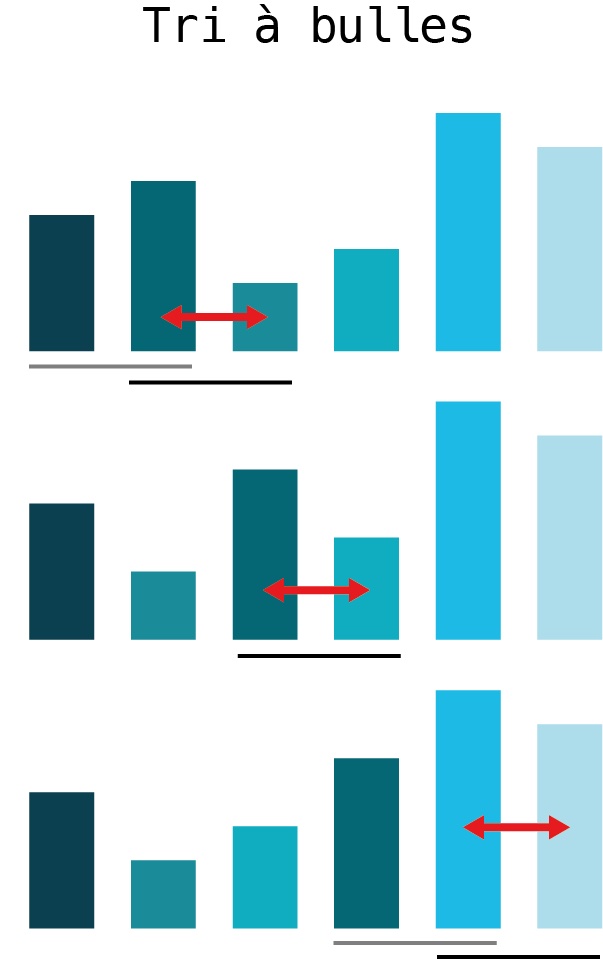
Voici une visualisation du tri à bulles.

Exercice : Modifiez la taille de la liste.